| ||||||||||||||||||||||||||||||||||||||||
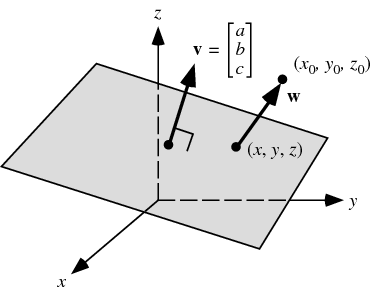 Given a plane
and a vector from the plane to the point is given by
Dropping the absolute value signs gives the signed distance,
which is positive if This can be expressed particularly conveniently for a plane specified in Hessian normal form by the simple equation
where Given three points
Then the distance from a point
where
as it must since all points are in the same plane, although this is far from obvious based on the above vector equation. |
I personally would like to post something relating to my own interests, such as my research interests(visual odometry, 3D reconstruction, segmentation, energy minimisation), hobbies(photography, cooking) ...
Tuesday 31 January 2012
How to calculate the distance between a arbitrary point to a plane?
Saturday 28 January 2012
4 new NAOs are joining our group
Hi everyone,
We just got 4 new "guys" involve our group. Actually they are really good at acting performance, even dance better than me.
Here is the video demo made by my colleague Inkyu Sa.
We just got 4 new "guys" involve our group. Actually they are really good at acting performance, even dance better than me.
Here is the video demo made by my colleague Inkyu Sa.
Subscribe to:
Posts (Atom)
![v=[a; b; c],](http://mathworld.wolfram.com/images/equations/Point-PlaneDistance/NumberedEquation2.gif)
![w=-[x-x_0; y-y_0; z-z_0].](http://mathworld.wolfram.com/images/equations/Point-PlaneDistance/NumberedEquation3.gif)